Diphthong Synthesis
Introduction
Diphthong production requires a swift transition of the vocal tract geometry from one vowel configuration to another within a short time frame. Accurately modeling these dynamic articulatory movements is crucial for natural-sounding speech synthesis and for the clinical assessment of voice quality. Numerous vocal tract acoustic models have been proposed in the literature; however, most focus on static tract geometries for producing isolated vowel sounds. Only recently have efforts been made to address dynamic articulatory configurations. In this work, we introduce a two-dimensional (2D) dynamic vocal tract model that employs the Immersed Boundary (IB) approach to synthesize diphthongs.
Mothod
Speech production involves the continuous movement of articulators—such as the jaw, lips, and tongue—that dynamically shape the vocal tract geometry. This dynamic geometry is typically represented by one-dimensional area functions, which describe the cross-sectional area of the vocal tract perpendicular to its centerline, extending from the glottis to the lips (as illustrated below). Accurately capturing these dynamic changes is particularly important for modeling diphthongs, which require smooth interpolation between distinct vowel configurations. Although high-fidelity Finite Element (FE) models (Arnela et al., 2019) can simulate these transitions with great precision, their high computational cost makes them impractical for real-time or large-scale applications. Alternatively, acoustic wave modeling approaches that employ regular domain discretization schemes—such as the Digital Waveguide Model (DWM) and Finite-Difference Time-Domain (FDTD) method—are computationally more efficient. For instance, Gully et al. (2017) used a 3D DWM and mapped admittance values of the airway boundaries onto a 3D rectilinear mesh. They then interpolated between vowel-specific admittance maps to synthesize diphthongs. However, the regular discretization of a computational domain using grid cells necessitates approximating the complex vocal tract boundaries in a stair-stepped manner, which does not accurately reflect their actual geometry. We propose a dynamic 2D vocal tract model that combines the standard 2D FDTD scheme with a unique IBM originally developed for large-scale virtual and room acoustic simulations (Bilbao, 2022).
Our proposed wave solver (2D IBM) is framed in terms of IBM within a 2D FDTD scheme using a dual set of discrete forcing terms in both the continuity and motion equations. As with classic IB methods, the acoustic wave equations are solved on a fixed Eulerian grid, while the dynamic vocal tract boundary is approximated using a fixed set of Lagrangian points as the immersed boundary. This approach eliminates the need for stair-stepped approximations of the geometry.
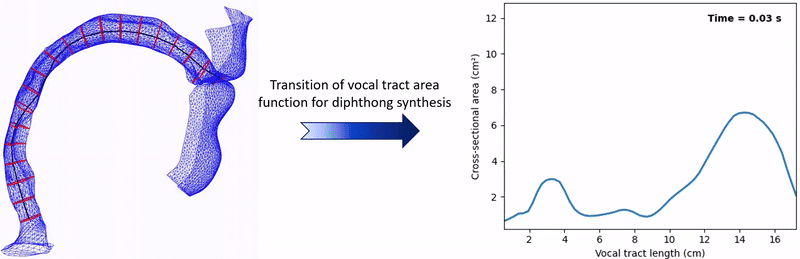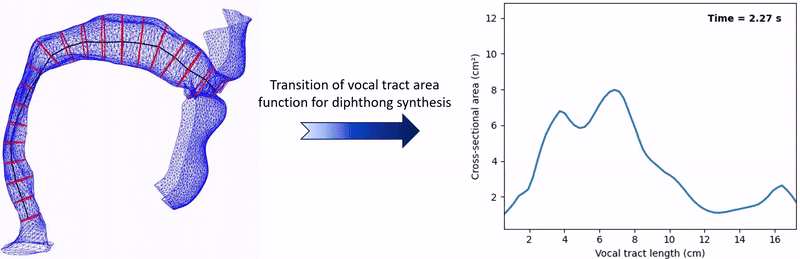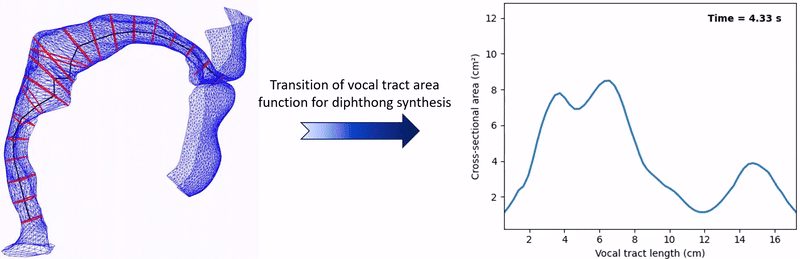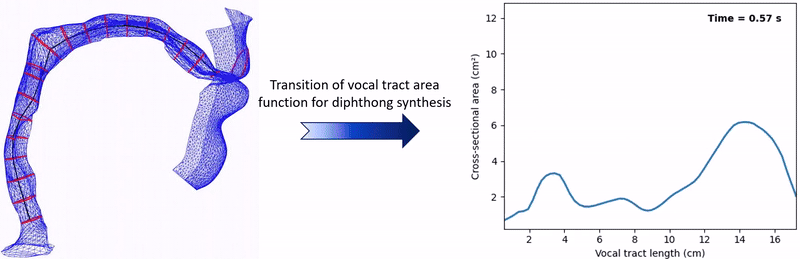
Synthesized Diphthongs
Synthesis of [ɔɪ] as in "boy"
Synthesis of [aʊ] as in "now"
Synthesis of [eɪ] as in "day"
References
[1] (Arenla et al., 2019) MRI-based vocal tract representations for the three-dimensional finite element synthesis of diphthongs.[2] (Gully et al., 2017) Diphthong synthesis using the dynamic 3D digital waveguide mesh.
[3] (Bilbao, 2022) Immersed boundary methods in wave-based virtual acoustics.